From the recursion-theory-is-fun dept.

Consider a language with support for lazy sequences (or streams). You get two streams, xs and ys, and you are asked to produce the cartesian product (cartesian xs ys) of the two streams. To be precise, the requirement is that the result is a stream that enumerates each pair [x y] where x is produced by xs and y is produced by ys.

Natural Numbers are Easy, Right?

Let us first try this in the case that xs and ys are each an enumeration of the natural numbers, starting from 0. Then (cartesian xs ys) is simply an enumeration of the set of pairs of natural numbers. It is easy to see that the naive implementation does not yield the correct result:

(def nat (iterate inc 0))

(def natXnat
  (for [x nat
        y nat]
    [x y]))

(take 10 natXnat)
  ;=> ([0 0] [0 1] [0 2] [0 3] [0 4] [0 5] [0 6] [0 7] [0 8] [0 9])

What has happened here? Sure enough, we do get a stream of distinct elements of (cartesian xs ys)—but somehow, the stream fails to enumerate any elements with a first component different from 0.

The reason is that a naive sequence comprehension like the above will simply traverse the right-hand side sequence for each element of the left-hand side sequence. Since the right-hand side sequence never terminates, the left-hand side sequence is never advanced.

Surely, we can do better. Let us plot the set we want to enumerate and try to come up with an enumeration sequence.

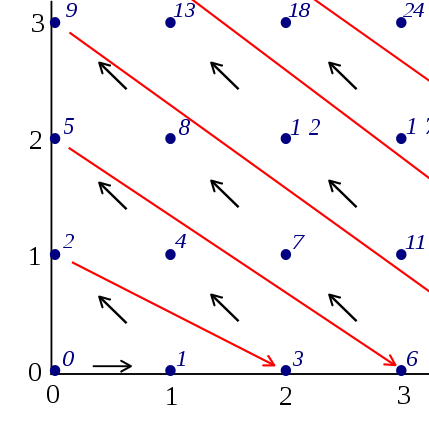
(Source: Wikimedia Commons)

The idea is rather simple. In the first step, we generate one element with x = 0. Next, we generate one element with x = 0 and one with x = 1. Next, we generate one element with x = 0, one with x = 1, one with x = 2. And so on.

Therefore, what we effectively have to do is enumerate the diagonals as illustrated in the picture above. We do this by starting at one end of a diagonal, and in each successive step, decrement the one component of the pair while incrementing the other. In more graphical terms, we take successively larger pairs of prefices (representing the parts of the axes that each diagonal encompasses) of the stream of natural numbers and traverse them in parallel, in opposing order.

For our natural number example, we can thus write the enumeration down as follows.

(def natXnat
  (letfn [(iter [a b]
            (lazy-seq
             (cons [a b]
                   (if (zero? b)
                     (iter 0       (inc a))
                     (iter (inc a) (dec b))))))]
    (iter 0 0)))

(take 10 natXnat)
  ;=> ([0 0] [0 1] [1 0] [0 2] [1 1] [2 0] [0 3] [1 2] [2 1] [3 0])

Much better!

(Note: You can use the inverse Cantor pairing function to generate the same sequence in a less recursive way. Also, see Christoph's post on countable sets for a more mathematical treatment.)

Generalizing the Method

Having done all that, how hard is it to generalize the procedure to arbitrary sets? It turns out that it is, while tricky in technical terms, quite easy to do the adaptation:

(defn cartesian [xs ys]
  (letfn [(reverse-prefices [items]
            (reductions conj nil items))]
    (let [xpres (reverse-prefices xs)
          ypres (map reverse (reverse-prefices ys))]
      (mapcat (fn [xprefix yprefix]
                (map vector xprefix yprefix))
              xpres
              ypres))))

This version of cartesian does essentially the same thing as the natural-number-specific one above in that it successively generates larger and larger subsequences and traverses them in parallel, one of them in natural order, the other in reverse.

Dealing with the Finite Case

If we only care about infinite sequences, we are done at this point. If we need to accomodate finite sequences as well, some technicalities arise, like having to skip pairs where one of the components would ordinarily be outside the range of one of the input sequences. The resulting definition looks a lot scarier than the one above, though it really does the same thing:

(defn cartesian [xs ys]
  (let [skip (gensym)]
    (letfn [(reverse-prefices [items]
              (reductions conj nil items))
            (pad [items]
              (lazy-cat items (repeat skip)))
            (skip? [x]
              (identical? skip x))]
      (let [xpres (rest (reverse-prefices (pad xs)))
            ypres (map reverse (rest (reverse-prefices (pad ys))))]
        (apply concat
               (take-while          ;deal with the finite case
                seq
                (map (fn [xprefix yprefix]
                       (filter (fn [pair] (not (some skip? pair)))
                               (map vector xprefix yprefix)))
                     xpres
                     ypres)))))))

It is an easy generalization to make the cartesian function accept an arbitrary (finite) number of input sequences. This is left as an exercise to the reader.